- 医療関係者向けホーム
- 医療関連情報
- 論文を正しく執筆するための統計学入門
- 論文を正しく執筆するための統計学入門 Vol.1
 統計学の
統計学の
基本概念
講師:杉本 典夫 先生(杉本解析サービス 代表)
前口上
さて皆さん、「数字は魔物、統計は数字のトリック」などといわれ、統計学は、ある人達からは疫病神のように忌み嫌われ、またある人達からは金科玉条のごとく無条件に信奉され、はたまた別の人達からは塵芥のごとく無視されています。しかし共通していえることは、統計学の本質が十分に理解されているとはいい難いのが現状ではないか?ということです。
色々な分野の研究者が統計手法を利用する時、誤って用いられていることがあります。私の印象では、その誤りの約90%は統計学の基本的な事柄であり、その原因は統計学の基本を十分理解していない、または誤解しているためではないかと感じています。
例えば研究現場における統計学3大間違いは、次のようなものではないでしょうか。
- 有意確率p値と「有意差あり」の意味
- 標準偏差(SD)と標準誤差(SE)の使い分け
- 多重比較の使用方法
これらはいずれも統計学の基本なのですが、残念なことに統計学の専門書はもちろん入門書の類にもあまり詳しく解説されていません(基本であるがゆえ、なのでしょうか)。
そこで実際に統計学を用いて論文を執筆する医学研究者の方はもちろんのこと、知識のアップデートや情報収集などのために研究論文を読む機会の多い医療従事者の方のために、統計学の基本的なことをできるだけ数式を使わず、できるだけやさしく解説したいと思います。
「私は統計学は遠慮しておきますよ。何しろ数学アレルギーでして…」
などといわず、少々お付き合いください。何しろアレルギーには減感作療法という治療法があるのですから!
 統計学と推計学
統計学と推計学
統計学とは
そもそも、統計学とは何か
「統計学とは、読んで字のごとく、統一して(統べて)計る学問である!」……などと、いきなり禅問答のようなことを申し上げましたが、統計学は沢山のデータを要約し、その中に含まれている情報を把握しやすくするための手段です。
例えば100名の日本人について血清尿酸値を測定したデータがあるとします。そうすると、当然、データが100個あるわけですが、数値の羅列であるそれらのデータを眺めただけで、「よしわかった、このデータに含まれている情報はこれこれである!」などと読み取ることは難しいと思います。
データに含まれる情報を読み取りやすくするには
情報を読み取りやすくするために、例えば平均値(mean)という値を求めます。平均値はこれら100個のデータのほぼ真ん中を表す値であり、100個のデータを1つに要約した値です。統計学では、このような要約値のことを統計量といいます。
さて、今、100個のデータの平均値が5.5mg/dLになったとします。そうするとこの値から、
「100個のデータはだいたい5.5mg/dLぐらいの値である」
つまり 「100名の日本人の血清尿酸値はだいたい5.5mg/dLぐらいである」
という情報を読み取ることができます。そしてこの情報に基づいて、次のような推測をすることができます。
「日本人の血清尿酸値はだいたい5.5mg/dLぐらいである」
このように100個のデータを平均値に要約することによって、データに含まれる情報が把握しやすくなりました。そしてその情報に基づいて、色々な推測をすることができます。つまり統計学はデータを要約して中に含まれている情報を把握しやすくするための手段なのです。
推計学とは
知っていますか?記述統計学と推測統計学(推計学)の違い
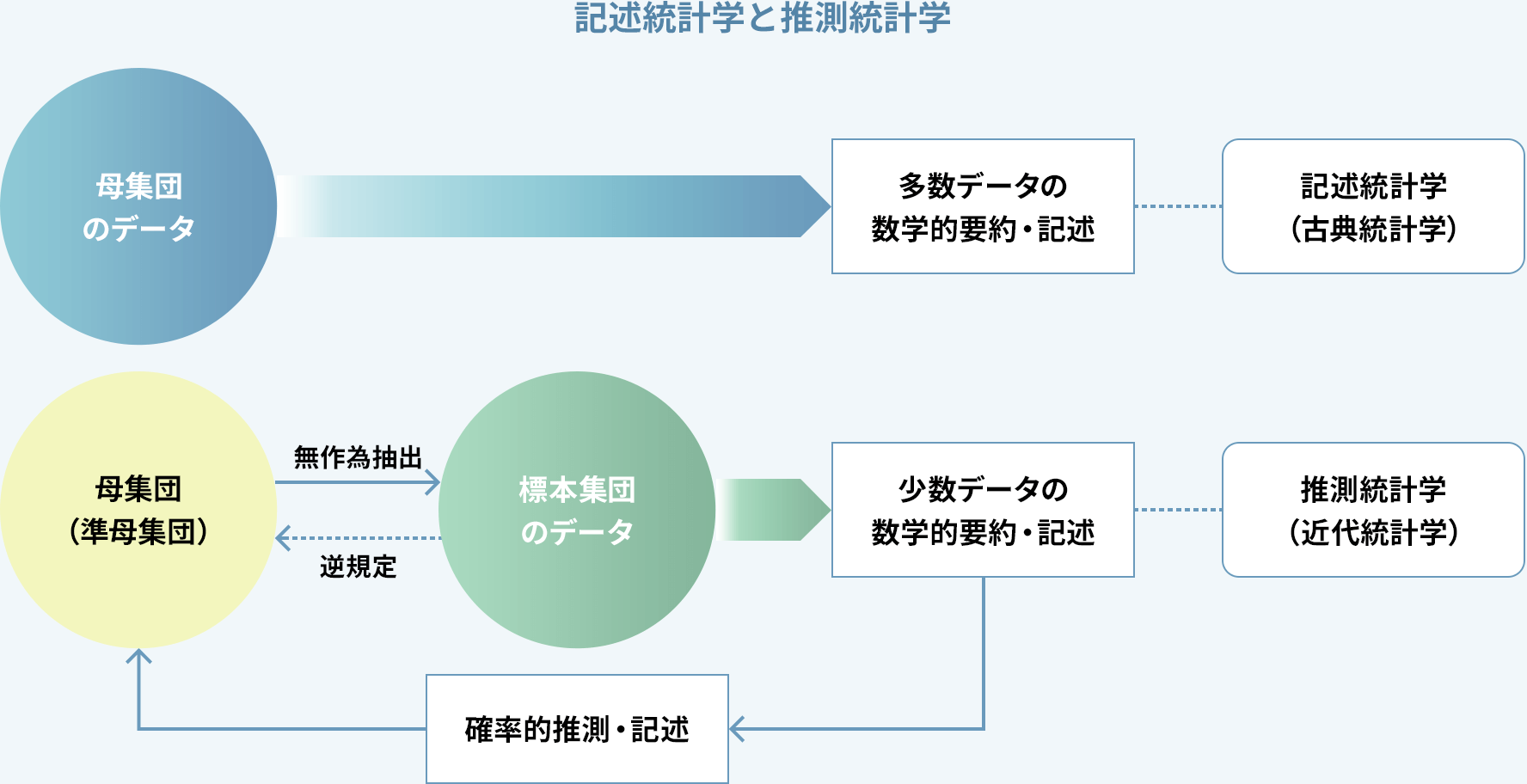
統計学には大きく分けて記述統計学(descriptive statistics)と推測統計学(inductive statistics)の2種類があります。推測統計学は推計学(stochastics)ともいわれ、以前はこの用語がよく使われていました。
記述統計学:母集団そのもののデータを活用
調査対象集団=母集団(population)のデータを要約し、母集団の情報を数学的に記述することが中心で、古典統計学とも呼ばれる。国勢調査で用いられる統計手法が代表例。
推測統計学(推計学):
標本集団の要約値から母集団の要約値を推測
母集団から無作為抽出した標本集団(sample)の要約値から母集団の要約値を確率的に推測し、それによって母集団の様子を数学的に記述することが中心で、近代統計学とも呼ばれる。科学実験や臨床試験で用いられる統計手法が代表例。
医学分野の臨床試験や臨床研究をはじめとして一般的な科学研究では、主として推測統計学が用いられます。しかし次に解説するように、医学分野の研究にはこの分野独特の特徴があります。
無作為抽出と準母集団
実は作為的な「無作為抽出」!?
推測統計学では、標本集団のデータに基づいて母集団の様子を確率的に推測します。そのため標本集団は、母集団の正しい代表になるように非常に注意深く選ばれなければなりません。そこで無作為抽出(random sampling)という標本抽出法が考案されました。
「無作為」というと、まるで「デタラメに」とか「いきあたりばったりに」標本を抽出するように思うかもしれません。しかし標本抽出法でいう「無作為」とは、「母集団を構成する個々の人または個体を等しい確率で抽出する」という意味です。そのため無作為抽出では母集団の中の特定の人または特定の個体に偏ることがないように、無作為どころか、乱数表などを使って大いに作為的に人または個体を選び出します。
アンケートを利用した世論調査などでは、対象とする母集団から標本集団を無作為抽出することが原理的には可能です。しかし医学の研究現場で行う実験や試験では、対象とする母集団から標本集団を無作為抽出することはほとんど不可能です。
例えば高尿酸血症患者を対象とした試験を行う場合、母集団は日本全体の高尿酸血症患者になります。その日本全体の高尿酸血症患者から標本集団を無作為抽出しようとすると、患者全員に番号を付けておき、乱数表などを利用して特定の患者を抽出することになります。しかし日本全体の高尿酸血症患者を全員特定することは事実上不可能です。また時間の経過とともに患者数は流動的に変化するため、母集団を正確に特定することも原理的に不可能です。
試験結果の違いは、「準母集団」の違いが原因の可能性も
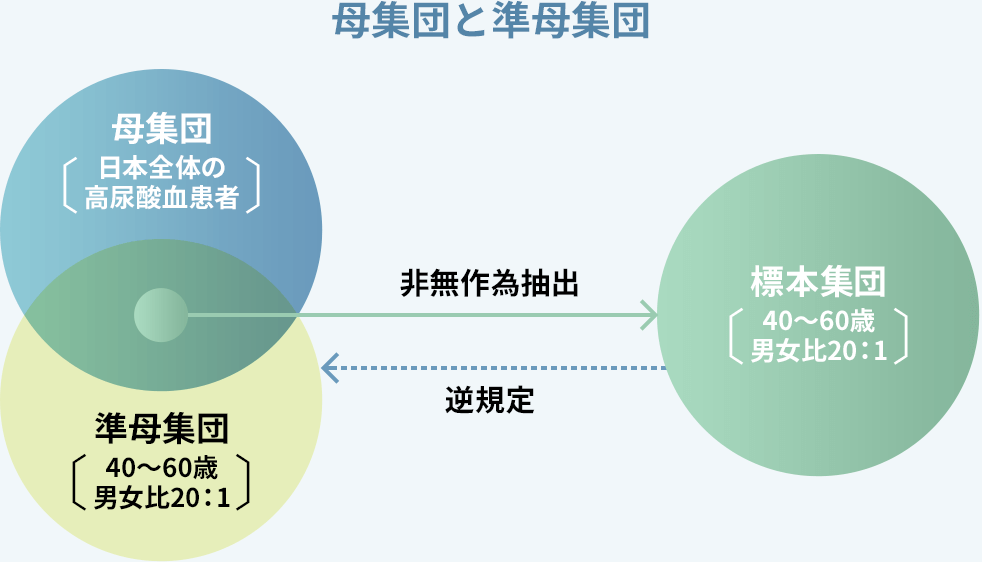
このような時は、たまたま集められた標本集団の背景因子(background factors)から母集団を逆に規定します。その母集団のことを準母集団(quasi-population)といいます。背景因子とは集団の特徴を表すような項目のことであり、性、年齢などの人口統計学的特性(demographic characteristics)が代表的です。
例えば、たまたま集めた高尿酸血症患者100名は年齢が40〜60歳であり、男女の比率が20対1だったとします。そうするとこの標本集団の準母集団は年齢が40〜60歳で、男女比が20対1という制限付きの集団になります。この制限付きの準母集団は日本人全体の高尿酸血症患者という真の母集団とは少し異なります。
同じような内容の試験を行っても、試験によって全く違った結果になり、その解釈に苦しんだり、議論の的になったりすることがよくあります。それは実は科学理論の問題ではなく、試験の準母集団の違いによることも多いようです。
試験のデータから得られた結論を適用できるのは、その試験の標本集団と同じ背景因子を持つ準母集団だけです。そのため同じような内容の試験でも、たまたま集められた標本集団の背景因子が異なり、その準母集団が異なっていれば違った結果になっても不思議ではありません。試験を行う研究者はこのことをしっかりと認識しておく必要があります。
今回は統計学の基本的な目的と統計学の種類、そして医学分野で統計学を用いる時の特殊性について紹介しました。
次回はデータを「見える化」する方法と、最も基本的な要約値である平均値と標準偏差、そして標準誤差について紹介する予定です。
講師プロフィール:杉本 典夫(杉本解析サービス 代表)
1975年静岡大学理学部化学科卒業。同年製薬会社入社、研究開発部に所属。解析室設置時には室長に就任。2006年株式会社セラノスティック研究所取締役、2008年杉本解析サービス開業。2014年より国立研究開発法人国立長寿医療研究センター客員研究員兼務。専門はデータの統計解析とソフトウェア開発。